原标题：基于st_bkinf集成学习的注塑件尺寸预测方法。2023新能源车成型及材料应用论坛

　　摘要：机器学习算法能够处理高维和多变量数据,并在复杂和动态环境中提取数据中的隐藏关系,在注塑件尺寸预测中具有很好的应用前景。注塑件尺寸预测系统的性能取决于机器学习算法的选择,然而,传统的机器学习算法在实际应用中不能达到很好的预测效果。为此,文中提出了一种基于st_bkinf集成学习的融合模型,首先采用优化的特征选择方法获得最佳的特征数量,然后通过对比分析单一模型的关联度和预测效果、不同st_bkinf学习器组合方式下模型的预测效果,得到预测性能最佳的模型,该模型的基学习器为极端梯度提升树(xCB)、轻量级梯度提升树(LCB)、核岭回归,元学习器为弹性网络回归。测试结果表明:该模型在注塑件尺寸预测方面的均方根误差和平均绝对误差较xCB和LCB模型分别降低了16%和20%左右,较传统支持向量机模型分别降低了45.22%和46.48%,同时模型预测结果可根据特征解释回溯到实际生产中,为制造工艺和工序的优化提供决策指导。

　　注塑成型作为最常见的一种塑料制品加工工艺,其所加工的产品在生活中随处可见,例如电子产品、汽车配件、玩具以及其他众多消费品[1]。由于注塑成型过程较为复杂且对环境比较敏感,加工过程中的不稳定因素会导致不良品的产生,造成经济损失[2]。同时,现有的注塑件质量检测大多采用人工,存在效率低和用工成本高等问题[3]。因此,相关研究通过建立注塑成型大数据,运用机器学习方法分析建模,对注塑件质量进行在线预测,以解决甚至避免现场痛点问题。

　　文献[4]通过构建多棵回归树,对每棵回归树的预测值取平均,组合所有的回归树即构成随机森林,来预测汽车注塑件的成型质量。文献[5]通过建立三层反向传播(BP)神经网络,利用Molcelow正交试验所得工艺参数与翘曲量的数据作为训练样本对神经网络进行训练,建立预测薄壳注塑件翘曲量的模型。文献[6]通过BP神经网络和径向基函数(RBF)神经网络建立预测注塑产品翘曲量的模型,并将两者的预测精度进行比较,从而得到有效的预测模型。文献[7]利用提取的故障特征数据与极端梯度提升树(xCB)集成算法训练出注塑机注射油缸内泄漏故障的智能诊断模型,并利用粒子群优化算法完成超参数的寻优。文献[8]利用加工过程中获得的数控系统内部指令域大数据,基于LM.BP神经网络与RBF神经网络学习实现零件尺寸的预测。

　　上述预测方法中,大部分只使用了传统的单一机器学习模型,或是简单模型的线性融合,模型整体预测精度较低,未能达到工业生产的要求。为此,本文提出了一种基于st_bkinf集成学习的融合模型,通过集成不同类型的学习器来提升模型的预测效果,并根据基学习器xCB提供的特征重要性排序方法,获得对注塑件尺寸影响程度较大的特征及其重要性排序,以期为制造工艺和工序的优化提供决策指导。

　　st_bkinf集成学习方法最初由wolpdrt[9]于1992年提出,经不断优化和改进,目前最完善的st_bkinf算法流程如图1所示。

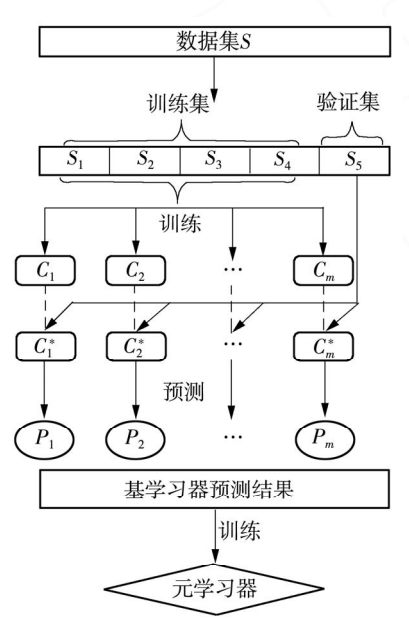
　　对于数据集s=│(Xi,yi),i=1,2,.,n,其中Xi为第i个样本的特征向量,yi为第i个样本对应的标签值,j为每个特征向量中的特征个数,即每一个特征向量Xi=(xi1,xi2,.,xij)。选取m个基学习器(C1,C2,.,Cm),采用K折交叉验证方法。

　　(2)将K-1折数据用于训练第一层的m个基学习器,在此过程中实现对基学习器的参数调整,可得到m个训练完毕的基模型C1*,C2*,…,Cm(*)。使用此m个训练完成的基模型预测剩余1折数据,得到预测结果P1,P2,…,Pm,形式为n/K行文m列。

　　(4)将步骤(3)得到的结果作为元学习器的输人,训练元学习器,输出结果为n行文1列数据,标签数据依旧是yi,在这个过程中实现对元学习器的参数优化。至此得到完整的训练完毕的st_bkinf集成学习模型。

　　与传统的Boostinf和B_ffinf集成学习方法相比,st_bkinf集成学习方法在步骤(4)中将基学习器的输出作为元学习器的输人,使元学习器能够整合全部基学习器的预测结果,并能减少第一层基学习器的预测偏差。通过这种方式集成不同类型的学习器,能结合不同学习器的优势,得到的信息更加全面,st_bkinf集成学习方法也因此有着更广泛的适用性[10]。

　　本文拟通过使用st_bkinf方法集成不同类型的学习器来提升模型的整体预测性能,从而使集成模型能达到更好的预测效果。

　　本文选用的数据集来源于第四届工业大数据创新竞赛决赛数据集,总计包含16600条数据,由成型机状态数据集和传感器高频采样数据集两个文件构成。成型机状态数据集来自成型机机台,均为表征成型过程中的一些状态数据,主要包括最小射胶位置、熔胶时间、熔胶背压、注射/保压切换压力、切换时间、切换位置、模具温度、充模时间、熔胶结束后冷却时间等。每一行对应一个模次,数据维度为86维。传感器高频采样数据集来自模温机及模具传感器采集的数据,主要包括模温机回水温度、射嘴压力、模温机水流量、模腔压力、模温机热水温度、模温机冷水温度等。文件夹内每一个模次对应一个bsv文件,单个模次时长为40~43s,含有24个传感器采集的数据。

　　对于成型机状态数据集,特征维度总计86维,其中缺失值特征7维,由于缺失值特征均为全部缺失,因此对缺失值进行删除操作。同时成型机状态数据集中存在3个特征(模次号Ic、记录时间spbTimd和备注Rdm_rk)对模型预测没有帮助,故将其删除,留下76维特征。

　　对于传感器高频采样数据集,总计24维特征,存在两个特征(采样时间s_mpldTimd和阶段Ph_sd)对模型预测没有帮助,故作删除处理,留下22维特征。尝试运用多种方式提取同一模次中的特征,包括提取中位数、最大值、最小值、众数等,选取相同的机器学习模型并参数调优后发现,提取均值得到的预测准确度最高。将预处理后的成型机状态数据集与传感器高频采样数据集组合,得到98维16600条数据的数据集,随机选取其中10000条数据用来训练和验证模型,6600条数据作为测试集。

　　特征选择和特征提取有着些许的相似点,这两者达到的效果是一样的,即试图减少特征数据集中特征的数目。但两者所采用的方法不同:特征提取主要是通过属性间的关系,如组合不同的属性得到新的属性,这样就改变了原来的特征空间;而特征选择是从原始特征数据集中选择出子集,是一种包含的关系,没有更改原始的特征空间。因此通过特征选择方法建立的模型具有良好的解释性,可以通过特征解释回溯到生产工序中。

　　本文选用过滤型特征选择方法中应用较为广泛的sdldbtKBdst方法,sdldbtKBdst方法有特征数量k和打分函数sbord两个参数。sbord的作用是给特征进行打分,然后从高到低选取特征,效果是移除得分前k名以外的所有特征。注塑件尺寸预测问题属于回归问题,因此sbord函数选用erdfrdssion回归函数。

　　选用轻量级梯度提升树(LCB)模型,使用5折交叉验证方法评估模型的预测精度,模型预测偏差(均方误差,MsE)随特征数量k变化的折线所示。由图中可得,特征数量为14时,模型预测偏差最低,因此sdldbtKBdst特征选择方法将特征维度降至14维。

　　回归模型的预测性能通过预测尺寸与实际尺寸的偏差来评估,最常用的评价指标有平均绝对误差(MAE,EMA)、均方误差(MsE,EMs)和均方根误差(RMsE,ERMs),计算公式如下:

　　为了使得st_bkinf模型的预测性能达到最优,既要选择合适的基学习器,又要选择恰当的元学习器,同时不同学习器之间的组合方式也至关重要。因此在建立st_bkinf模型时,需要立足于各个模型的预测能力与各模型之间的相关度展开分析,选择合适的基学习器、元学习器及其组合方式,才能建立有效的st_bkinf模型。

　　本文初步选择的基学习器有树(Trdd)、随机森林(RF)、梯度提升决策树(CBDT)、xCB、LCB、弹性网络回归(ENdt)、核岭回归(KRR)、支持向量机(sVM)。其中,Trdd有着良好的预测性能和成熟的理论支撑,在很多领域得到了较好的应用。RF和CBDT分别使用B_ffinf和Boostinf的集成方法对Trdd进行改进,在预测性能方面有了较大的提升。xCB模型有最强机器学习算法之称,LCB模型对xCB模型的生长策略和过拟合问题进行了优化[11]。xCB和LCB模型在对Trdd使用Boostinf集成的基础上,又借鉴了B_ffinf集成方法进行随机采样,是融合使用Boostinf和B_ffinf集成方法的典范。ENdt和KRR模型是针对线正则化的改进模型,有严谨的理论支撑和出色的实践应用效果。sVM模型对于解决小样本、非线性及高维度的问题有独特的优势,在工业领域已经得到了十分广泛的应用。

　　在进一步选择第一层的基学习器时,要综合考虑两个方面:一是因为st_bkinf模型的有效性主要来自于特征抽取[12],而不同的算法是从不同的数据空间角度来抽取特征的,因此要尽量选择差异度较大的模型作为基学习器,才能最大程度地综合不同算法的优势[13];二是学习能力强的基模型有助于整体预测效果的提升[14],单独预测性能非常好的基模型能在很大程度上提升融合模型的最终预测性能,因此要尽量选择学习能力强的基模型。

　　模型之间的差异可以用各模型预测结果的关联度来表示。本文使用Pd_rson相关系数分析不同模型的关联程度,计算式如下:

　　式中,μx和μy分别为模型x和模型y的预测均值。根据式(3)计算得到的结果,画出各模型之间的相关性矩阵热力图,如图3所示。热力图中颜色越深,模型之间的相关系数越接近1,相关程度越强;反之,模型之间的相关系数越接近0,相关程度越弱。

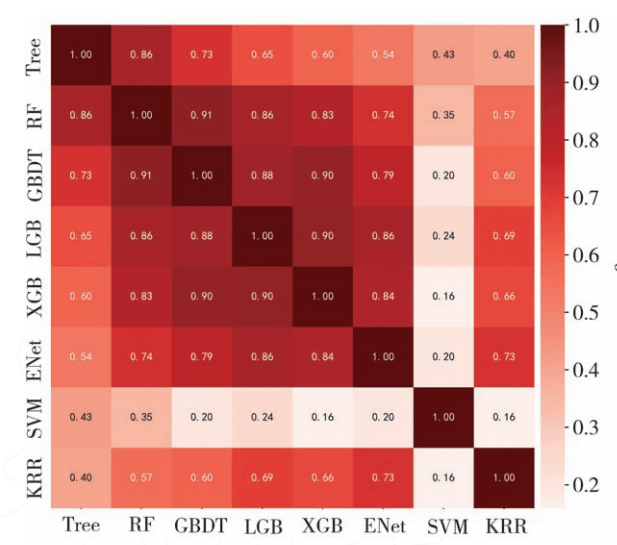
　　从图3中可知:Trdd、RF、CBDT、LCB、xCB模型两两之间的相关度都很高,因为这几个模型虽然在训练机理上有些不同,但本质都是基于决策树的优化算法,算法观测数据空间的角度差异很小;KRR模型是基于线性模型的改进模型,与树模型的关联度较低;sVM与上述模型的原理有着较大的差异,因此跟其他模型的预测结果相关度也很。